二年级

1.有一列数：1,2,3,4,5,6……

(1)从1—75共有多少个数?

(2)1—75之间有多少个数?

解答：(1)75个数。(2)74-1=73个。

2.找规律填数。

(1)1,3,5,7,9,(),(),15,17

(2)40,35,30,25,(),(),10,5

解答：(1)一个比一个大2，填11、13。

(2)一个比一个小5，填20、15。

三年级

1.如图，○、□、△分别代表不同的数字，那么它们分别代表什么?

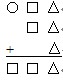
解答：通过个位可以判断出来，△只能是0或5。如果△=0，那么□也只能为0。所以△=5，□=9，○=8。

2.某月有31天，有4个星期二和4个星期五，那么这个月的20日是星期几?

解答：1、8、15、22、29是一组，2、9、16、23、30是一组，3、10、17、24、31是一组，这些都不可能是星期二或星期五。从1号到7号一定是一周，1、2、3号都不可能是星期二或星期五，那么只能在4号到7号之间，因此只能4号是星期二，7号是星期五。20号与6号一样，所以是星期四。

四年级

1.在下面竖式中，有若干个数字被遮盖住了，竖式中被遮盖住的几个数字之和是多少?

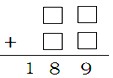
解答：个位相加没有进位，和就是9，十位相加是18，一定是9+9=18，因此这几个数字的和是18+9=27。

2.在下面的算式中，三个加数的数字都被遮住了，被遮住的几个数字之和是多少?

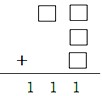
解答：想法一：个位最多进2，十位是9加进位会有一个进位，因此题目中会有3个进位，3×9=27，27+1+1+1=30。

想法二：十位只有9+2=11，个位最多进2，个位一定是相加满21，可能是6+7+8，也可能是5+7+9，还可能是9+9+3等等，无论是几，和都是21，第一个加数的最高位一定是9，因此9+21=30。

五年级

1.在一张节目单中原有9个节目，若保持这些节目相对顺序不变，再添加进去3个节目，则所有不同的添加方法共有多少种?

解答：现有的9个节目正好有10个空，加进去的3个节目中，第一个节目有10个空可以选。插入之后就变成了11个空，所以第二个节目有11个空可以选。同理，第三个节目有12个空可以选，因此共有10×11×12=1320种。

2.有一类自然数，从第三个数字开始，每个数字都恰好是它前面两个数字之和，直至不能再写为止，如257，1459等等，这类数共有多少个?

解答：前两位数的和应不大于9。当前两位数确定后，就惟一确定了一个这类数，所以求这类数的个数，等于求前两位数有多少种。第一位数可取1—9，当第一位数是n时，第二位数可以是0—(9-n)的任一个，所以这类数共有9+8+7+……+2+1=45个。

六年级

1.小华买圆珠笔若干支，正好付出10元钱，他所买的圆珠笔有两种，有1元1支的，也有1元5角一支的，他两种圆珠笔各买了多少支?

解答：设1元的买了x支，1元5角的买了y支

x+1.5y=10

解得x=7,y=2或x=4,y=4或x=1,y=6

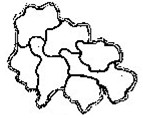
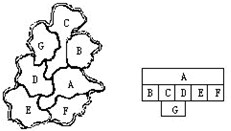
2.某沿海城市管辖7个县，这7个县的位置如图。现用红、黑、绿、蓝、紫五种颜色染色，要求任意相邻的两个县染不同颜色。共有多少种不同的染色方法?三年级

解答：把该沿海城市地图上的7个县分别编号为A、B、C、D、E、F、G(如左图)。为了便于观察，可以把左图改画成右图(相邻关系不改变)。由于与A相邻的区域最多，所以从A考虑，按A、B、C、D、E、F、G的顺序，用红、黑、绿、蓝、紫五种颜色依次染色，根据乘法原理，共有5×4×3×3×3×3×3=4860(种)不同的染色方法。

解答：