二年级

1.动物园在5个铁丝笼子里养了15只猴子，但每个笼子里的猴子数不一样，你知道每个笼子里该有多少只猴子吗?

解答：15=1+2+3+4+5

2.小林家养了一只大白兔和一只小花猫，有一天，小林抱着大白兔站在体重计上称一称，正好是12千克，后来小林放下大白兔，又抱起小花猫站在体重计上称一称，正好是10千克;最后小林把大白兔和小花猫一起放在体重计上称是4千克。请问小林、大白兔和小花猫各是多少千克?

解答：大白兔比小花猫重12-10=2千克，而它们俩一共重4千克，所以大白兔是3千克，小花猫是1千克，小林的体重为12-3=9千克。

三年级

1.草地上有黑兔、白兔、灰兔共12只，黑兔比白兔多2只，灰兔比白兔少2只。黑兔、白兔、灰兔各有多少只?

解答：黑兔比白兔多2只，白兔比灰兔多2只，所以假设把两只黑兔变成灰兔，那么三种兔子就一样多了，所以白兔有12÷3=4只，黑兔有4+2=6只，灰兔有4-2=2只。

2.下图是用12根小棒组成的4个同样大小的正方形，请你移动3根小棒，使原图形变成3个同样大小的正方形。想一想，应怎样移?

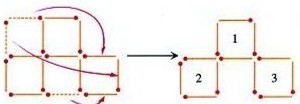
四年级

1.小强、小明、小勇三个人参加数学竞赛，他们分别来自甲、乙、丙三个学校，并分别获得一、二、三等奖。已知：

(1)小强不是甲校选手;

(2)小明不是乙校选手;

(3)甲校选手不是一等奖;

(4)乙校的选手得二等奖;

(5)小明不是三等奖;

根据上述情况，可判断出小勇是哪个学校的选手?他得的是几等奖?

假设小明是甲校的，那么小明不是一等奖，只能是二等奖，与第4个条件冲突，因此小明是丙校的，小勇是甲校的，小强是乙校的。小强就是二等奖，小明是一等奖，小勇是三等奖。

2.有一个有余数的除法算式中，商是41，余数是3，被除数、除数、商和余数的和是1055，被除数是多少?

解答：被除数与除数的和为1055-41-3=1011，而被除数比除数的41倍多3，因此除数为(1011-3)÷(41+1)=24，被除数为1011-24=987。

五年级

1.张三说李四在说谎，李四说王五在说谎，王五说张三和李四都在说谎。问：张三、李四、王五3个人到底谁说的是真话，谁说的是谎言?

解答：假设张三说的是对的，那么李四在说谎，那么王五说的是对的，与假设矛盾。

假设李四说的是对的，那么王五和张三都说谎了，符合条件。

假设王五说的对的，那么张三和李四都在说谎，矛盾。

因此李四说的是对的，张三和王五全说谎了。

2.某班的一次数学考试中，平均成绩是78分，男、女生各自的平均成绩是75.5分和81分。问：男生人数是女生人数的多少倍?

解答：平均每个男生比平均分少2.5分，平均每个女生比平均分多3分，因此6个男生少的分数可以用5个女生多的分数补回来。6÷5=1.2倍。

六年级

1.从甲地到乙地原来每隔45米要装一根电线杆，加上两端的两根，一共有53根电线杆，现在改成每隔60米装一根电线杆，除两端的两根不需要移动外，中途还有多少根不必移动?

解答：45与60的最小公倍数是180，因此每隔180米的电线柑不用移动。甲乙两地之间距离为(53-1)×45=2340，因此有2340÷180+1=14根不用移动。

2.由1，3，4，5，7，8这六个数字所组成的六位数中，能被11整除的最大的数是多少?

解答：数字和为1+3+4+5+7+8=28，因此奇数位与偶数位的数字和之差可以为0或22。如果是0，那么奇数为与偶数位数字和都是14，最大为875413。如果是22，那么奇数位与偶数位数字和分别为25和3，显然不成立。因此最大为875413。