2011年公务员联考《行测》:鸡兔同笼问题探讨
编辑:
2011-07-19
二、下面我们通过2010年国家公务员考试真题来进一步强化“方程法”
例1、某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位,甲教室每排可坐10人,乙教室每排可坐9人。两教室当月共举办该培训27次,每次培训均座无虚席,当月培训1290人次。问甲教室当月共举办了多少次这项培训?()(2010年国家公务员考试行测第48题)
A.8B.10C.12D.15
【答案】D 解析:本题中可设甲教室举办X次培训,乙教室举办Y次培训,根据人数列方程,

由方程我们可以得出题的答案。
例2、已知甲、乙两种产品原价之和为100元,因市场变化,甲产品8折促销,乙产品提价10%,价格调整之后,两种产品的标价之和比原标价之和提高了4%,则乙产品的原标价为多少元( )
A.20B.40C.80D.93
【答案】C 解析:本题中可设甲产品原价为X元,乙产品原价为Y元,根据甲乙标价之和前后比方程,
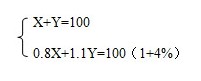
例3、某班35人外出春游,老师给了小明88元买冰激凌,买了两种口味,如果买20只巧克力味和15个草莓味的就差2元,买15个巧克力20个草莓的剩下3元,一只草莓味道的多少钱( )
A.4B.3 C.2D.1.5
【答案】C 解析:本题中可设巧克力味冰激凌为X元,草莓味冰激凌为Y元,列方程:

例4、有蜘蛛、蜻蜓、蝉三种生物共18只,共有腿118条,翅膀20对(蜘蛛8条腿,没有翅膀;蜻蜓有6条腿,2对翅膀;蝉有6条腿和1对翅膀)求蝉有几只?( )
A.5B.6 C.7D.8
【答案】B 解析:本题中可设蜘蛛X只,蜻蜓Y只,蝉Z只,列方程:

方程法解答鸡兔同笼问题比较直观,比如例4的题目涉及到三种物品时,假设法就很复杂了,但是采用方程法很简单的求出结果。
以上是关于鸡兔同笼问题的几种解题思路,从中找到适合自己的方式,并能将一般问题转化成鸡兔同笼问题是对考生的基本要求。
我个人倾向采用二元一次方程法解答鸡兔同笼问题,因为列方程的等式关系显而易见,并且不会出错,但是存在解方程费时的缺点。很多人认为采用“假设法”解答鸡兔同笼问题能在最短的时间里解出,但是存在需要记忆公式并解答的问题。所以希望考生们多做此类问题,找到适合自己的并能很快得出答案的方法。
在线测试:
更多试题请进入:51自学网
标签:数量关系
免责声明
威廉希尔app (51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。