初中常用公式:推导公式整理
来源:51EDU威廉希尔app 编辑:sx_wangha
2018-09-14 15:03:53
推导公式一文为大家除了整理了推导公式,还为考生朋友们提供了推到常见练习题,希望可以帮到大家~
推导公式
tanα+cotα=2/sin2α
tanα-cotα=-2cot2α
1+cos2α=2cos^2α
1-cos2α=2sin^2α
1+sinα
=(sinα/2+cosα/2)^2
=2sina(1-sin2a)+(1-2sin2a)sina
=3sina-4sin3a
cos3a
=cos(2a+a)
=cos2acosa-sin2asina
=(2cos2a-1)cosa-2(1-sin2a)cosa
=4cos3a-3cosa
sin3a
=3sina-4sin3a
=4sina(3/4-sin2a)
=4sina[(√3/2)2-sin2a]
=4sina(sin260°-sin2a)
=4sina(sin60°+sina)(sin60°-sina)
=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]
=4sinasin(60°+a)sin(60°-a)
cos3a
=4cos3a-3cosa
=4cosa(cos2a-3/4)
=4cosa[cos2a-(√3/2)2]
=4cosa(cos2a-cos230°)
=4cosa(cosa+cos30°)(cosa-cos30°)
=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}
=-4cosasin(a+30°)sin(a-30°)
=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]
=-4cosacos(60°-a)[-cos(60°+a)]
=4cosacos(60°-a)cos(60°+a)
上述两式相比可得
tan3a=tanatan(60°-a)tan(60°+a)
[page]推到练习题及答案
1、如图所示,有一个正方体形的铁丝架,把它的侧棱中点I、J、K、L也用铁丝连上.
(1)现在一个蚂蚁想沿着铁丝从A点爬到G点,问最近的路线一共有几条?并用字母把这些路线表示出来(用所经过的连接点字母表示,譬如蚂蚁从A点出发,经过I点L点,最后到达H点,这样的路线用AILH表示).
(2)蚂蚁是否可能从A点出发,沿着铁丝经过每一个连接点恰好一次,最后到达G点?如果可能,请找出一条这样的路线;如果不可能,说明为什么?
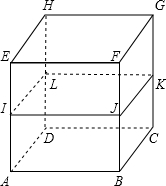
(1)一共有12条:ABCKG、ABJKG、ABJFG、ADCKG、ADLKG、ADLHG、AIJKG、AIJFG、AILKG、AILHG、AIEFG、AIEHG;
(2)不可能.
用反证法证明.假设可能,那么将所有连接点染上黑、白两色,凡与黑点相邻的都是白点,凡与白点相邻的都是黑点.
若A是白点,则黑白点的分布如下表:

由于A与G都是白点,所以蚂蚁从A点出发,依次经过其它各点,到达G点的路线应为白→黑→白→黑→…→黑→白.其中有奇数个白点,这与图中共有偶数个白点相矛盾.
∴蚂蚁不可能从A点出发沿着铁丝经过每一个连接点恰好一次,最后到达G点.
2、如图,可数出直角三角形______个.
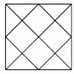
以正方形的顶点为直角三角形的直角顶点的直角三角形有4×2=8个.
∴直角三角形共有12+8=20个.
故答案为20.
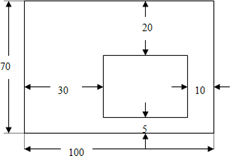
3、某工艺品厂要从一块矩形的石板中截断的方式割出一块与原矩形各边分别平行的较小的矩形石板(如图),“截断切割”是指每次割沿一条直线将石板切割成两块.设切割的成本与切割长度成正比,那么,共有多少种成本不同的切割顺序?( )A.12B.14C.18D.24
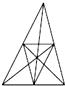
(b)能否在平面上画出7条直线(任意三条都不共点),使得它们中的每条直线都恰与另三条直线相交?如果能请画出一例,如果不能请简述理由.
答案:(a)在平面上画三条平行的直线m1,m2,m3,再画另三条平行的直线n1,n2,n3,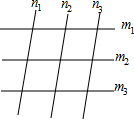 使它们与前一组平行线相交.
使它们与前一组平行线相交.
(b)在平面上不能画出没有三线共点的七条直线,使得其中每条直线都恰与另外三条直线相交.
理由如下:假设平面上可以画出没有三线共点的七条直线,
其中每一条直线都恰与另外三条相交,两直线相交只有一个交点,
∴每条直线上恰有另三条直线交得的三个不同的交点,
∴七条直线共3×7=21个交点,
∵每个交点分属于两条直线,重复计数一次,
∴这七条直线交点数为
| 21 |
| 2 |
推导公式一文就为朋友们提供到此,本文还为大家提供了三倍角公式、锐角三角函数公式、和差化积公式等,想要获得更多信息请时刻关注我们~
- 2019-03-06 17:09:27
- 2019-03-06 16:09:00
- 2019-03-06 15:08:03
- 2019-03-06 14:26:30
- 2019-03-06 13:23:04
- 2019-03-06 11:13:55
- 2019-03-06 10:07:29
- 2019-03-06 09:38:58
- 2019-03-04 16:18:37
- 2019-03-04 15:15:23
免责声明
威廉希尔app (51edu.com)在建设过程中引用了互联网上的一些信息资源并对有明确来源的信息注明了出处,版权归原作者及原网站所有,如果您对本站信息资源版权的归属问题存有异议,请您致信qinquan#51edu.com(将#换成@),我们会立即做出答复并及时解决。如果您认为本站有侵犯您权益的行为,请通知我们,我们一定根据实际情况及时处理。
- [原创]初一数学下册思维导图:整式的乘...
- [原创]初一数学下册思维导图:相交线与...
- [原创]初一数学下册思维导图:三角形知识点
- [原创]初一数学思维导图:变量之间的关...
- [原创]初一数学下册思维导图:生活中的...
- [原创]初一数学下册知识点:概率初步
- [原创]初一数学知识点:代数初步知识点
- [原创]初一数学知识点:有理数知识点
- [原创]初二政治:丰富的社会生活知识点
- [原创]人教版初二政治:网络生活新空间...